[CS231n] 3. Optimization

Keyword : Stochastic Gradient Descent

 

 

1) Introduction

Two key components in context of the image classification task:

1. A (parameterized) score function mapping the raw image pixels to class scores (e.g. a linear function)
2. A loss function that measured the quality of a particular set of parameters based on how well the induced scores agreed with the ground truth labels in the training data.(e.g. Softmax/SVM).

 

---

 

2) Optimization

The process of finding the set of parameters W that minimize the loss function.

 

Strategy #1 : Random Search

Very bad idea solution

• Simply try out many different random weights and keep track of what works best.

# assume X_train is the data where each column is an example (e.g. 3073 x 50,000)
# assume Y_train are the labels (e.g. 1D array of 50,000)
# assume the function L evaluates the loss function

bestloss = float("inf") # Python assigns the highest possible float value
for num in xrange(1000):
  W = np.random.randn(10, 3073) * 0.0001 # generate random parameters
  loss = L(X_train, Y_train, W) # get the loss over the entire training set
  if loss < bestloss: # keep track of the best solution
    bestloss = loss
    bestW = W
  print 'in attempt %d the loss was %f, best %f' % (num, loss, bestloss)

# prints:
# in attempt 0 the loss was 9.401632, best 9.401632
# in attempt 1 the loss was 8.959668, best 8.959668
# in attempt 2 the loss was 9.044034, best 8.959668
# in attempt 3 the loss was 9.278948, best 8.959668
# in attempt 4 the loss was 8.857370, best 8.857370
# in attempt 5 the loss was 8.943151, best 8.857370
# in attempt 6 the loss was 8.605604, best 8.605604
# ... (trunctated: continues for 1000 lines)

 

We can take the best weights W found by this search and try it out on the test set

# Assume X_test is [3073 x 10000], Y_test [10000 x 1]
scores = Wbest.dot(Xte_cols) # 10 x 10000, the class scores for all test examples
# find the index with max score in each column (the predicted class)
Yte_predict = np.argmax(scores, axis = 0)
# and calculate accuracy (fraction of predictions that are correct)
np.mean(Yte_predict == Yte)
# returns 0.1555

• brain-dead random search solution

→ iterative refinement

• Our new approach will be to start with a random W and then iteratively refine it, making it slightly better each time.

 

Strategy #2 : Random Local Search

• Try to extend one foot in a random direction and then take a step only if it leads downhill.
• A random W, generate random perturbations δW to it and if the loss at the perturbed W+δW is lower, we will perform an update.

W = np.random.randn(10, 3073) * 0.001 # generate random starting W
bestloss = float("inf")
for i in range(1000):
  step_size = 0.0001
  Wtry = W + np.random.randn(10, 3073) * step_size
  loss = L(Xtr_cols, Ytr, Wtry)
  if loss < bestloss:
    W = Wtry
    bestloss = loss
  print 'iter %d loss is %f' % (i, bestloss)

• Still wasteful and computationally expensive.

 

Strategy #3 : Following the Gradient

• There is no need to randomly search for a good direction:
• We can compute the best direction
• This direction will be related to the gradient of the loss function.

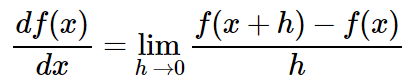
• In multiple dimensions, the gradient is the vector of (partial derivatives) along each dimension
• The slope in any direction is the dot product of the direction with the gradient. The direction of steepest descent is the negative gradient

 

---

 

3) Computing the gradient

3.1) Numerical Gradient

A slow, approximate but easy way. Need to loop over all dimensions

def eval_numerical_gradient(f, x):
  """ 
  a naive implementation of numerical gradient of f at x 
  - f should be a function that takes a single argument
  - x is the point (numpy array) to evaluate the gradient at
  """ 

  fx = f(x) # evaluate function value at original point
  grad = np.zeros(x.shape)
  h = 0.00001

  # iterate over all indexes in x
  it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
  while not it.finished:

    # evaluate function at x+h
    ix = it.multi_index
    old_value = x[ix]
    x[ix] = old_value + h # increment by h
    fxh = f(x) # evalute f(x + h)
    x[ix] = old_value # restore to previous value (very important!)

    # compute the partial derivative
    grad[ix] = (fxh - fx) / h # the slope
    it.iternext() # step to next dimension

  return grad

• The code above iterates over all dimensions one by one, makes a small change h along that dimension and calculates the partial derivative of the loss function along that dimension by seeing how much the function changed.
• The variable grad holds the full gradient in the end.

# to use the generic code above we want a function that takes a single argument
# (the weights in our case) so we close over X_train and Y_train
def CIFAR10_loss_fun(W):
  return L(X_train, Y_train, W)

W = np.random.rand(10, 3073) * 0.001 # random weight vector
df = eval_numerical_gradient(CIFAR10_loss_fun, W) # get the gradient

The gradient tells us the slope of the loss function along every dimension, which we can use to make an update:

loss_original = CIFAR10_loss_fun(W) # the original loss
print 'original loss: %f' % (loss_original, )

# lets see the effect of multiple step sizes
for step_size_log in [-10, -9, -8, -7, -6, -5,-4,-3,-2,-1]:
  step_size = 10 ** step_size_log
  W_new = W - step_size * df # new position in the weight space
  loss_new = CIFAR10_loss_fun(W_new)
  print 'for step size %f new loss: %f' % (step_size, loss_new)

# prints:
# original loss: 2.200718
# for step size 1.000000e-10 new loss: 2.200652
# for step size 1.000000e-09 new loss: 2.200057
# for step size 1.000000e-08 new loss: 2.194116
# for step size 1.000000e-07 new loss: 2.135493
# for step size 1.000000e-06 new loss: 1.647802
# for step size 1.000000e-05 new loss: 2.844355
# for step size 1.000000e-04 new loss: 25.558142
# for step size 1.000000e-03 new loss: 254.086573
# for step size 1.000000e-02 new loss: 2539.370888
# for step size 1.000000e-01 new loss: 25392.214036

 

3.1.1) Update in negative gradient direction

Making an update in the negative direction of the gradient since we wish our loss function to decrease, not increase.

 

3.1.2) Effect of step size

Choosing the step size (also called the learning rate) will become one of the most important (and most headache-inducing) hyperparameter settings in training a neural network.

• If we shuffle our feet carefully we can expect to make consistent but very small progress (this corresponds to having a small step size).
• We can choose to make a large, confident step in an attempt to descend faster, but this may not pay off.(overshoot and make the loss worse)
  → at some point taking a bigger step gives a higher loss as we “overstep”.

 

3.1.3) A problem of efficiency

Modern Neural Networks can easily have tens of millions of parameters.

Clearly, this strategy is not scalable and we need something better.

 

 

3.2) Analytic Gradient

A fast, exact but more error-prone way that requires calculus

 

3.2.1) Computing the Gradient Analytically with Calculus

• The numerical gradient is very simple to compute using the finite difference approximation
  → It is very computationally expensive to compute.
• Analytic gradient using Calculus, which allows us to derive a direct formula for the gradient (no approximations) that is also very fast to compute.
  → Unlike the numerical gradient it can be more error prone to implement
• In practice, Always use analytic gradient, but check implementation with numerical gradient. This is called a gradient check.

 

---

 

4) Gradient Descent

The procedure of repeatedly evaluating the gradient and then performing a parameter update

• Example : Vanilla Gradient Descent - the core of Neural Network libraries

# Vanilla Gradient Descent

while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # perform parameter update

• Gradient Descent is currently by far the most common and established way of optimizing Neural Network loss functions.

 

4.1) Mini-batch gradient descent

• In large-scale applications, the training data can have on order of millions of examples.
• It seems wasteful to compute the full loss function over the entire training set in order to perform only a single parameter update.
  → Compute the gradient over batches of the training data.

 

• Example : batch contains 256 examples from the entire training set of 1.2 million

# Vanilla Minibatch Gradient Descent

while True:
  data_batch = sample_training_data(data, 256) # sample 256 examples
  weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
  weights += - step_size * weights_grad # perform parameter update

• The reason this works well is that the examples in the training data are correlated.

• Full sum expensive when N is large
• Approximate sum using a minibatch of examples 32/64/128 common
  → powers of 2 in practice because many vectorized operation implementations work faster when their inputs are sized in powers of 2.

 

4.2) Stochastic Gradient Descent (SGD)

The extreme case of setting where the mini-batch contains only a single example.

• Also sometimes called on-line gradient descent
• This is relatively less common to see because in practice due to vectorized code optimizations it can be computationally much more efficient to evaluate the gradient for 100 examples, than the gradient for one example 100 times.