[CS231n] 2. Linear Classification

Keywords : Support Vector Machine, Softmax

parameteric approah, bias trick, hinge loss, cross-entropy loss, L2 regularization

---

Intro of Linear Classification

• In the last section we introduced the problem of Image Classification.
  
  
• K-Nearest Neighbor (kNN) classifier - it has a number of disadvantages.
  → The classifier must remember all of the training data and store it for future comparisons with the test data.
  → Classifying a test image is expensive since it requires a comparison to all training images.
  
  
• Develop a more powerful approach to image classification
  
  1. Score Function
  → maps the raw data to class scores
  
  2. Loss Function
  → quantifies the agreement between the predicted scores and the ground truth labels
  
  3. Optimization
  → minimize the loss function
  

---

1.1) Linear Score Function

Parameterized mapping from images to label scores

• Define the score function that maps the pixel values of an image to confidence scores for each class.

• Example

 

• The parameters in W are often called the weights, and b is called the bias vector because it influences the output scores, but without interacting with the actual data x
  
  
• Notice
  1. The single matrix multiplication Wxi is effectively evaluating 10 separate classifiers in parallel (one for each class), where each classifier is a row of W.
  2. We think of the input data (xi, yi) as given and fixed, but we have control over the setting of the parameters W, b.
  3. Our goal will be to set these in such way that the computed scores match the ground truth labels across the whole training set.
  4. Training data is used to learn the parameters W, b, but once the learning is complete we can discard the entire training set
     → New test image can be simply forwarded through the function and classified based on the computed scores.
     → faster than comparing a test image to all training images
     
     

---

1.2) Interpreting a linear classifier

• A linear classifier computes the score of a class as a weighted sum of all of its pixel values across all 3 of its color channels(RGB).

An example of mapping an image to class scores. For the sake of visualization, we assume the image only has 4 pixels (4 monochrome pixels, we are not considering color channels in this example for brevity), and that we have 3 classes (red(cat), purple(dog), green(ship) class). (Clarification: in particular, the colors here simply indicate 3 classes and are not related to the RGB channels.) Stretch the image pixels into a column and perform matrix multiplication to get the scores for each class. Note that this particular set of weights W is not good at all: the weights assign our cat image a very low cat score. In particular, this set of weights seems convinced that it's looking at a dog.

 

1.2.1) Analogy of images as high-dimensional points

• Since the images are stretched into high-dimensional column vectors, we can interpret each image as a single point in this space.
  ex) each image in CIFAR-10 is a point in 3072-dimensional space of 32x32x3 pixels
• Analogously, the entire dataset is a (labeled) set of points.
• Since we defined the score of each class as a weighted sum of all image pixels, each class score is a linear function over this space.

Cartoon representation of the image space, where each image is a single point, and three classifiers are visualized. Using the example of the car classifier (in red), the red line shows all points in the space that get a score of zero for the car class. The red arrow shows the direction of increase, so all points to the right of the red line have positive (and linearly increasing) scores, and all points to the left have a negative (and linearly decreasing) scores.

• We change one of the rows of W, the corresponding line in the pixel space will rotate in different directions.
• The biases b, on the other hand, allow our classifiers to translate the lines.

 

1.2.2) Interpretation of linear classifiers as template matching

• Each row of W corresponds to a template for one of the classes.
• We are still effectively doing Nearest Neighbor, but instead of having thousands of training images we are only using a single image per class
• we use the (negative) inner product as the distance instead of the L1 or L2 distance.

 

Example learned weights at the end of learning for CIFAR-10. Note that, for example, the ship template contains a lot of blue pixels as expected. This template will therefore give a high score once it is matched against images of ships on the ocean with an inner product.

• The horse template seems to contain a two-headed horse, which is due to both left and right facing horses in the dataset.
• The linear classifier merges these two modes of horses in the data into a single template.
• The template that has to identify cars, ended up being red, which hints that there are more red cars in the CIFAR-10 dataset than of any other color.
• The linear classifier is too weak to properly account for different-colored cars

 

1.2.3) Bias Trick

Combine the two sets of parameters into a single matrix

• The matrix holds both of them by extending the vector x_i with one additional dimension that always holds the constant 1 - a default bias dimension.

 

1.2.4) Linear Classifier : Three Viewpoints

 

 

---

 

2) Loss Function

Measure our unhappiness with outcomes, referred to as the Cost Function or the objective

• The loss will be high if we’re doing a poor job of classifying the training data, and it will be low if we’re doing well.

• There are several ways to define the details of the loss function.

 

2.1) Multiclass Support Vector Machine loss (SVM)

The SVM “wants” the correct class for each image to a have a score higher than the incorrect classes by some fixed margin Δ

• The SVM loss function wants the score of the correct class y_i to be larger than the incorrect class scores by at least by Δ (delta)
  
  
• Example

• Q1. What happens to loss if car scores change a bit?
  - still 0 loss (Feature of SVM hinge loss : Insensitive to data changes)
  
  
• Q2. What is the min/max possible loss?
  - min : 0, max : infinite
  
  
• Q3. At initialization W is small so all s ~ 0. What is the loss?
  - Sanity Check : class - 1 → use for debugging

 

• Q4. What if the sum was over all classes?(including j = y_i)
  - We want 0 loss, but if the sum is over all classes, loss is increase as much 1.

• Q5. What if we used mean instead of sum?
  - no matter. Just scale gets smaller
  
  
• Q6. What if we used squared hinge loss
  • Squared hinge loss SVM (or L2-SVM), which uses the form max(0,−)^2 that penalizes violated margins more strongly (quadratically instead of linearly).
  • The unsquared version is more standard, but in some datasets the squared hinge loss can work better. This can be determined during cross-validation.

 

Q. Suppose that we found a W such that L = 0. Is this W unique?
→ No! 2W is also has L = 0

→ How do we choose between W and 2W?

The Multiclass Support Vector Machine "wants" the score of the correct class to be higher than all other scores by at least a margin of delta. If any class has a score inside the red region (or higher), then there will be accumulated loss. Otherwise the loss will be zero. Our objective will be to find the weights that will simultaneously satisfy this constraint for all examples in the training data and give a total loss that is as low as possible.

 

2.2) Regularization

We wish to encode some preference for a certain set of weights W over others to remove ambiguity.
→ Regularization Penalty R(W)
→ The most common regularization penalty is the L2 norm that discourages large weights through an elementwise quadratic penalty over all parameters

 

Why Regularize?

• Express preferences over weights
• Make the model simple so it works on test data
• Improve optimization by add curvature

→ This effect can improve the generalization performance of the classifiers on test images and lead to less overfitting.

• Due to the regularization penalty we can never achieve loss of exactly 0.0 on all examples, because this would only be possible in the pathological setting of W=0.

 

2.3) Softmax Classifier

Unlike the SVM which treats the outputs f(xi, W) as (uncalibrated and possibly difficult to interpret) scores for each class, the Softmax classifier gives a slightly more intuitive output (normalized class probabilities) and also has a probabilistic interpretation

• Cross-entropy loss

 

• Softmax function

 

 

 

2.3.1) Information theory view

The cross-entropy between a “true” distribution p and an estimated distribution q is defined as:

 

• The Softmax classifier is hence minimizing the cross-entropy between the estimated class probabilities ( q=efyi/∑jefj as seen above) and the “true” distribution, which in this interpretation is the distribution where all probability mass is on the correct class (i.e. p=[0,…1,…,0] contains a single 1 at the yi -th position.)

 

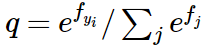
• Since the cross-entropy can be written in terms of entropy and the Kullback-Leibler divergence as

 

and the entropy of the delta function p is zero, this is also equivalent to minimizing the KL divergence between the two distributions (a measure of distance).

 

 

2.3.2) Probabilistic interpretation

• It can be interpreted as the (normalized) probability assigned to the correct label y_i given the image x_i and parameterized by W.
• We are therefore minimizing the negative log likelihood of the correct class, which can be interpreted as performing Maximum Likelihood Estimation (MLE).

 

• Q1. What is the min/max possible loss L_i?
  - min : 0, max : infinite
• Q2. At initialization all s will be approximately equal; what is the loss?
  - log(C) or -log(1/C), C : class → Sanity Check

 

 

2.3.3) Softmax vs. SVM

• Softmax classifier provides “probabilities” for each class.

A : At SVM, the result is not that different. But at Softmax, the probabilities are changed
→ SVM : insensitive, Sotfmax : sensitive

 

 

How do we find the best W?

→  Optimization